
With that being said, we’ll take a closer look at 20 must-know Sudoku tips and tricks to help beginners get started and play Sudoku the right way. It requires logical thinking, patience, and an organized mindset. Once a beginner player understands the objective of the game and learns a few of the techniques in figuring out the solution, the game is one merely of logic. Playing Sudoku requires minimal mathematical or scientific knowledge. In fact, it can be a highly rewarding experience that leaves you with a sense of achievement. Starting out as a Sudoku beginner doesn’t have to be a headache. What appears to be a complex mathematics game is actually a logic based game that is a lot easier than you think – when you know what to do.
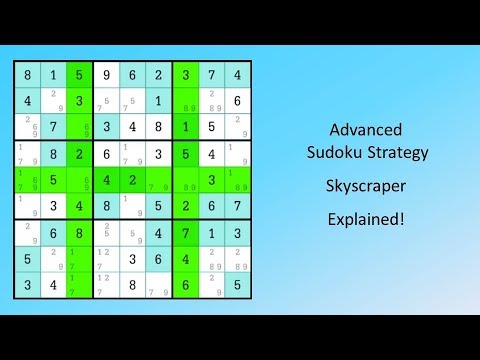
It is using different situations that will lead to a dead end and then removing the pencil-mark that lead to that dead end.If your interest in Sudoku has been recently sparked, you probably want to get started soon. This can fall under a more advanced technique but is in fact an excellent way of removing pencil-mark digits. Strategy #5: Testing Pencil-mark in Different Situations You can use this knowledge when combining other strategies like triples or hidden triples in this example. While the other 2 will either be a 3-6 or 4-5 (if you didn't have that green 4 already there). That means there MUST be a 7, 8, and 9 in that row. Well, they both have 3 common digits 7-8-9. Thus permanently eliminating 3 and 6 from any box in the row.Īnother strategy that needs to be considered is that you notice the 2 sums that add up to 33: 3-6-7-8-9 or 4-5-7-8-9. Now if you already know that one of the boxes is a 4 (due to the 7 over 3 lets say.) then you know the other 4 boxes will contain a 5-7-8-9 not a 3-6-7-8-9, Then you can eliminate combos based on the digits you already have filled in.įor Example, a 5 digit sum of 33 is either a 3-6-7-8-9 or 4-5-7-8-9. This strategy used is how you can further eliminate pencil marks.įirst, you make a list of all the combos that would add up to a given sum. Strategy #4: Combo Elimination / Common Digits Within Sums
SUDOKU STRATEGY FULL
Since (1,5) are only in box #2 and box #5 and (1,5) are not in any other boxes, then you can eliminate 2,3,4 from those two boxes.Įxample B can also be called a Triple since (2,3,4) are in 3 of the 5 boxes and therefore cannot be in the 2 boxes that also contain the (1,5).ĭepends on how you look at it, is the glass half full or half empty? In Example B: we have something known as a "Hidden Pair". If the 3rd box was set as a 5 for example, it would cause an obvious error in the row since you are not allowed to have the same digit in a row or column. The reason behind this is that the first box must be a 1 or a 5 and the second box must be a 1 or a 5. In Example A: if a box of a given row (or column) only has a pencil mark of (1,5) and another box in the same row (or column) also has a pencil mark of (1,5) then you can remove 1 and 5 from all other boxes in that row. The idea is to identify lone pairs, triples, and quadruples in a given row (or column) and eliminate those digits from the other boxes. This is a very good strategy when using pencilmarks.
*** Using pencilmarks will come in handy especially for the medium and hard levels. Then, as more clues are revealed, you can reduce the pencil marks until only one digit remain and that will be the digit used for that box. You don't need to over do it sometimes but it is good for a small range.
Using pencil marks, it is best to fill in possible values that you know are going to exist in a particular box.

Now, it seems like I am stating the obvious but it very easy to overlook it and think "I got it, it is no big deal" only to run into a problem later on. This strategy is best when starting off a puzzle.Īlthough it may take extra work, using pencil marks not only greatly reduce the chance for error, it helps to point out obvious hints in solving puzzles. Therefore, the only common value for the intersecting box is a 9. If a row has a sum of 16 over 2 squares and a column has a sum of 17 over 2 squares, the only possible values are 7-9 for the row and 8-9 for the column. In this article I will give you a few Sudoku strategies and will use the term rows for the across boxes and column for the down boxes. But keep in mind, in a Sudoku puzzle there is only one unique solution that will work successfully. This can get to a point where it almost looks impossible to solve and may take a long time using a variety of strategies. When the simple techniques don't work, you will need to use a more complicated solving technique. There are many techniques in solving a Sudoku puzzle. Five Beginner/Intermediate Sudoku Solving Strategies


 0 kommentar(er)
0 kommentar(er)
